Classification of Signals

Classification of Signals

  signals are classified into following categories:

• Continuous Time.
•  Discrete Time Signals.
• Deterministic and Random Signals.
• Even and odd Signals.
• Periodic and a Non-periodic Signals.
• Energy and Power signals.
• Real and Imaginary Signals.
• causal and Non-causal Signals.

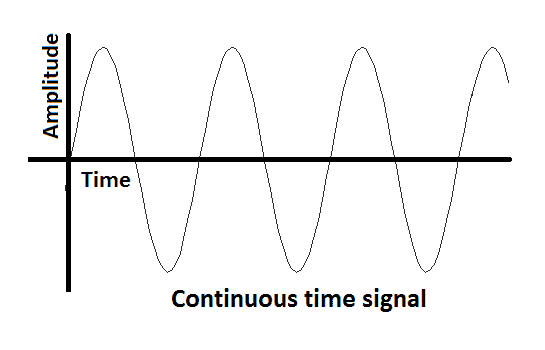
Continuous Time Signal.

The signal that are defined for every instants of time are known as Continuous Time Signal.

Continuous Time signal is also called analog signal. For continuous time signal dependent variable is time.

Discrete Time Signal. 

The signal that are defined only at discrete instants of time are known as Discrete Time Signal.

The discrete time signal are continuous in time but discrete in time. For discrete time signals, the independent variable is time (n). 

Deterministic and Random Signal.

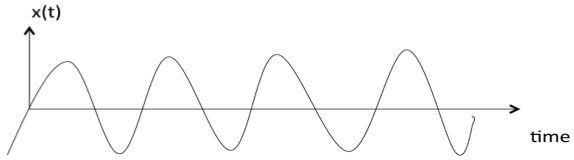
A signal is said to be deterministic if there is no uncertainty with respect to its value at any instant of time. Or, signals which can be defined exactly by a mathematical formula are known as deterministic signals.

Examples: sine wave, Exponential signal, Square wave, Triangular wave.

 

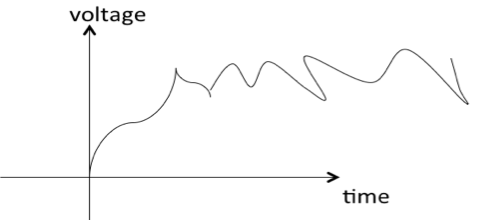
A signal is said to be Random Signal(Non-deterministic) if there is uncertainty with respect to its value at some instant of time. Random Signal(Non-deterministic) signals are random in nature hence they are called random signals. Random signals cannot be described by a mathematical equation. 

Examples: Thermal noise generated in an electric circuit. Such noise has a probabilistic in nature.

  

Even and Odd Signal.

A signal is said to be even when it satisfies the condition x(t) = x(-t). Even signal can be easily spotted as they are symmetric around the vertical axis.

 Example: t2, t4… cost etc.

Let x(t) = t2
x(-t) = (-t)2 = t2 = x(t)
∴,$\therefore ,$ t2 is even function.

A signal is said to be odd when it satisfies the condition x(t) = -x(-t)
Examples: t, t3 ... And sin t
Let x(t) = sin t
(-t) = sin(-t) = -sin t = -x(t)
∴,$\therefore ,$ sin t is odd function.


Any function ƒ(t) can be expressed as the sum of its even function ƒe(t) and odd function ƒo(t).
ƒ(t ) = ƒe(t ) + ƒ0(t )
where
ƒe(t ) = ½[ƒ(t ) +ƒ(-t )] 

Periodic and Non-periodic Signal

A signal which has a definite pattern and which repeats itself at regular intervals of time is called Periodic signal. mathematically, a continuous -time signal is called periodic signal.

x(t+T0 )=x(t) ...............for -∞<t<∞

where t=time      T=constant representing the period.

A signal which does not repeat at regular interval of time is called  Non-periodic or A periodic signal.

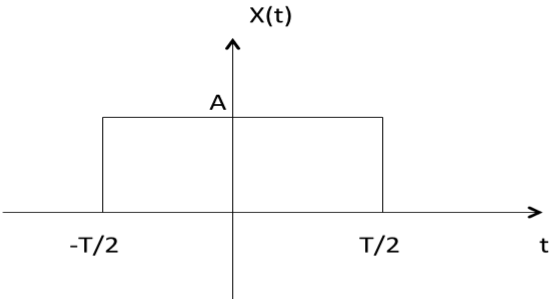
Energy and Power signal.

A signal is said to be energy signal when it has finite energy. But energy signal have  values

only in limited time duration.

Examples: a signal  having only one square pulse in energy signal. 

A signal is said to be power signal when it has finite power. A power signal is not limited in time.

It always exists from beginning to end and it never ends.

the power of an energy signal is 0, because of dividing finite energy by infinite time.

Example: Sine wave in infinite length is power signal.

A signal cannot be both, energy and power simultaneously. Also, a signal may be neither energy nor power signal.

Power of energy signal = 0
Energy of power signal = ∞

Real and Imaginary Signal

A signal is said to be real when it satisfies the condition x(t) = x*(t).

Example: If x(t)= 3 then x*(t)=3*=3 here x(t) is a real signal.

A signal is said to be odd when it satisfies the condition x(t) = -x*(t)

Example:If x(t)= 3j then x*(t)=3j* = -3j = -x(t) hence x(t) is a odd signal.

 For a real signal, imaginary part should be zero. Similarly for an imaginary signal, real part should be zero.

Causal and Non- causal signal

A system is said to be causal system if its output depends on present and past inputs only and not on future inputs.
Example:The output of casual system depends on present and past inputs, it means y(n) is a function of x(n), x(n-1), x(n-2), x(n-3)…etc. Some examples of causal systems are given below:
  y(n) = x(n) + x(n-2)
  y(n) = x(n-1) – x(n-3)
  y(n) = 7x(n-5)

Significance of causal systems:

Since causal system does not include future input samples; such system is practically realizable.  Generally all real time systems are causal systems; because in real time applications only present and past samples are present.
Since future samples are not present; causal system is memoryless system.

Non-causal system

A system whose present response depends on future values of the inputs is called as a non-causal system.
Examples:In this case, output y(n) is function of x(n), x(n-1), x(n-2)…etc. as well as it is function of x(n+1), x(n+2), x(n+3), … etc. following are some examples of non-causal systems:
     Y(n) = x(n) + x(n+1)
     Y(n) = 7x(n+2)
     Y(n) = x(n) + 9x(n+5)

Significance of Non-causal system:
Since non-causal system contains future samples; a non-causal system is practically not realizable. That means in practical cases it is not possible to implement a non-causal system.

Blog From

55.vivek Magre

56.Neha Jadhav

57.latif Punekar

58.Swati more

59.Aditya sabale.